Deep Representation Learning with Target Coding AAAI'15

Introduction

We consider the problem of learning deep representation when target labels are available. In this paper, we show that there exists intrinsic relationship between target coding and feature representation learning in deep networks. Specifically, we found that distributed binary code with error correcting capability is more capable of encouraging discriminative features, in comparison to the 1-of-K coding that is typically used in supervised deep learning. This new finding reveals additional benefit of using error-correcting code for deep model learning, apart from its well-known error correcting property. Extensive experiments are conducted on popular visual benchmark datasets.

Contribution Highlights

• We present the first attempt to analyse systematically the influences of target coding to feature representation.
• We show that the error-correcting Hadamard code encompasses some desired properties that are beneficial for deep feature learning.
• We validate the coding scheme with detailed examination of feature representation in each hidden layer of a deep model. Extensive experiments demonstrate that error correcting codes are beneficial for representation learning.

Citation

1. Deep Representation Learning with Target Coding
   S. Yang, P. Luo, C. C. Loy, K. W. Shum, X. Tang
   in Proceedings of AAAI Conference on Artificial Intelligence, 2015 (AAAI, Oral, nominated as easily accessible paper)
   PDF Supplementary Material Code

Images

Is 1-of-K the best target coding?

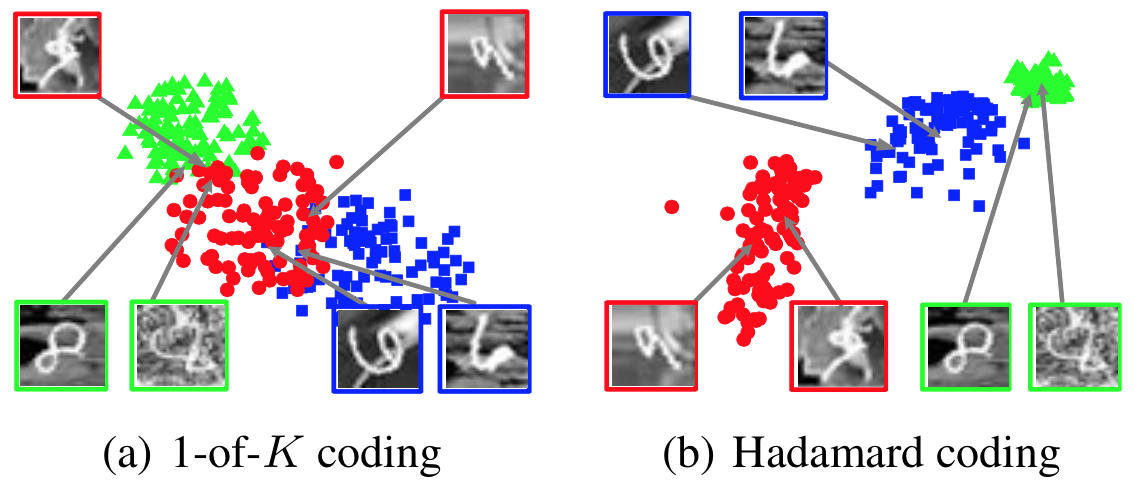
To examine the feature representation when a deep model is trained with different coding schemes, we project the features extracted from a deep convo- lutional neural network’s penultimate layer to a two-dimensional embedding using multi-dimensional scaling. Hadamard coding is capable of separating all visually ambiguous classes {9, 8, 6}, which are confused in 1-of-K coding.

Target codes for representing different visual classes.

In the paper we demonstrate what one could achieve by replacing 1-of-K with the Hadamard code (Langford and Beygelzimer 2005) as target vectors in deep feature learning.

The CNN structure used in our experiments.

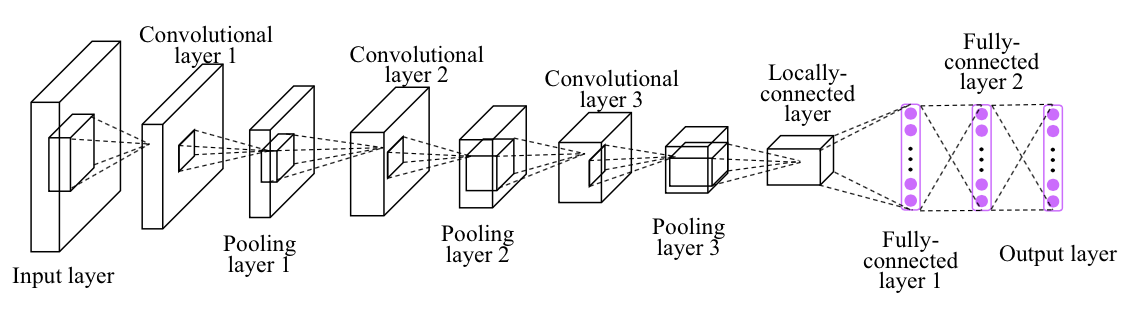
As the Hadamard code is independent to a network structure, any other deep models can be employed as well.

The change of features observed when applying 1- of-K and the Hadamard coding:

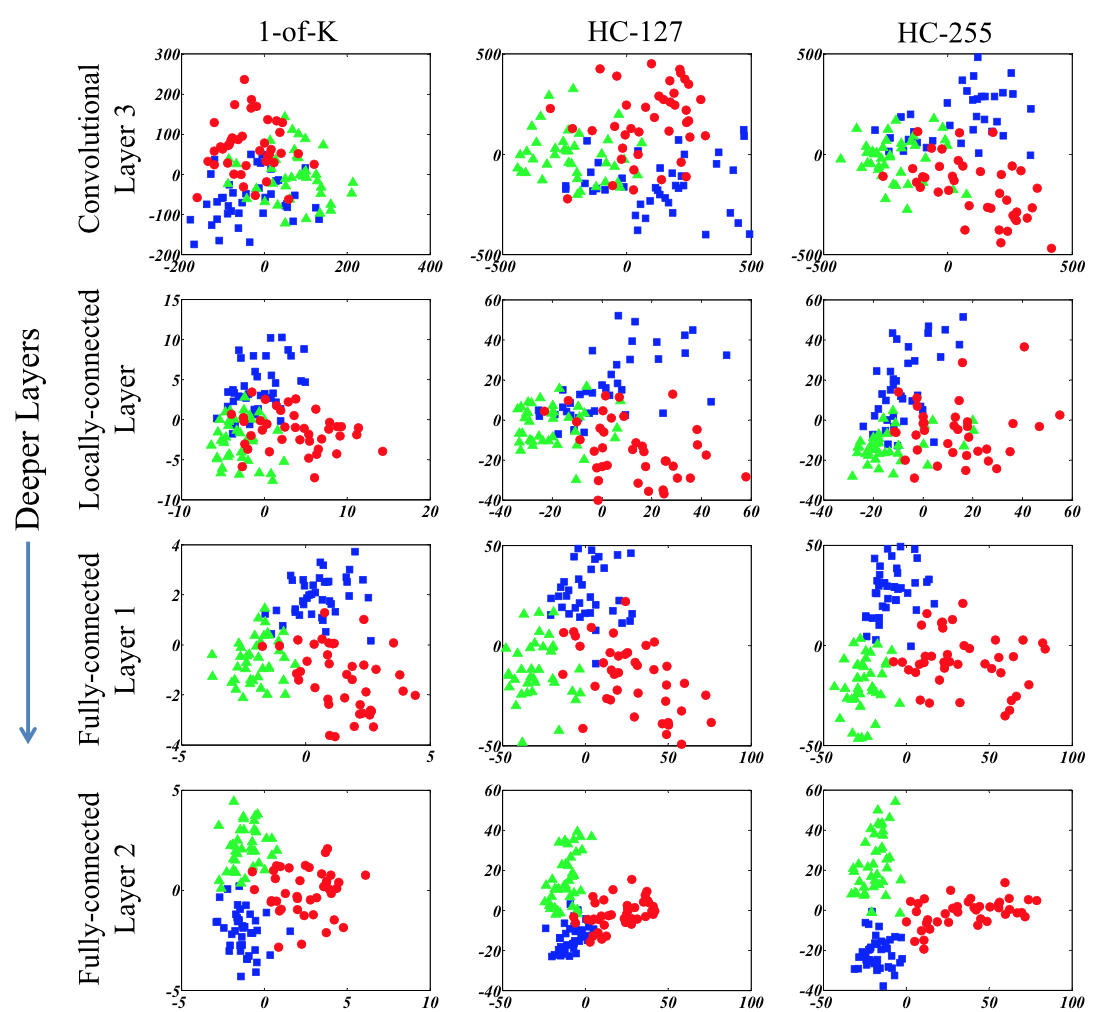
We deliberately choose three visually ambiguous classes {tiger, lion, leopard} from CIFAR- 100, indicated by red, green, blue, respectively. We extracted the features from different CNN layers, namely convolution layer 3, locally-connected layer, and fully-connected layers 1 and 2. To examine the feature representation given different coding schemes, we project the features to a two-dimensional embedding using multi-dimensional scaling. We compare 1-of-K against the Hadamard code with length 127 and 255 (HC-127 and HC-255). It is observed that the Hadamard code yields better data factorization than 1-of-K coding. Longer Hadamard code leads to more separable and distinct feature clusters.

The Hadamard code performs the best among different methods.

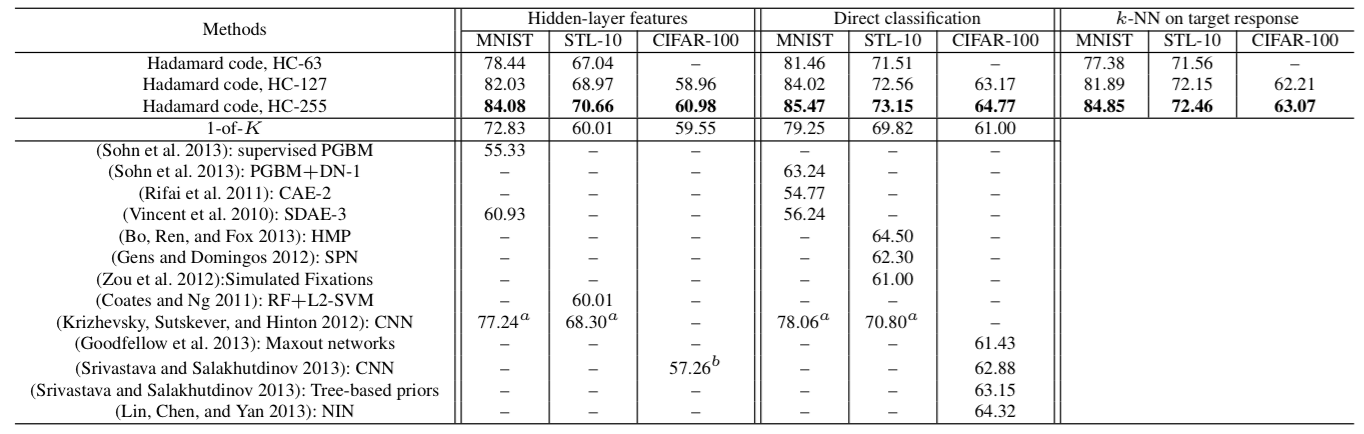
Classification accuracy (%) on MNIST, STL-10, and CIFAR-100. The best performers in each column are in bold. The Hadamard code and 1-of-K schemes employed the same CNN structure.

Some CIFAR-100 classification results by CNN trained with 1-of-K, HC-127, and HC-255.

It can be observed that despite 1-of-K performs well on easy instances, e.g. apple and butterfly, its performance is inferior than the Hadamard coding-based CNN, when applied to difficult classes like raccoon and chimpanzee.